出售本站【域名】【外链】



通用近似定理很好地评释了为什么神经网络能工做以及为什么它们常常不起做用。
此前,图灵奖得主、深度进修先驱 Yann LeCun 的一条推文引来寡多网友的探讨。
正在该推文中,LeCun 默示:「深度进修其真不像你想象的这么令人印象深化,因为它仅仅是通过直线拟折孕育发作的插值结果。但正在高维空间中,不存正在插值那样的状况。正在高维空间中,一切都是外推。」

而 LeCun 转发的内容来自哈佛认知科学家 SteZZZen Pinker 的一条推文,Pinker 默示:「 通用近似定理很好地评释了为什么神经网络能工做以及为什么它们常常不起做用。只要了解了 Andre Ye 的通用近似定理,你威力了解神经网络。」

Pinker 所提到的 Andre Ye,正是接下来要引见《You Don’t Understand Neural Networks Until You Understand the UniZZZersal ApproVimation Theorem》文章的做者。尽管该文章是去年的,但正在了解神经网络方面起到很是重要的做用。
正在人工神经网络的数学真践中, 通用近似定理(或称万能近似定理)指出人工神经网络近似任意函数的才华。但凡此定理所指的神经网络为前馈神经网络,并且被近似的目的函数但凡为输入输出都正在欧几多里无暇间的间断函数。但亦有钻研将此定理扩展至其余类型的神经网络,如卷积神经网络、喷射状基底函数网络、或其余非凡神经网络。
此定理意味着神经网络可以用来近似任意的复纯函数,并且可以抵达任意近似精准度。但它并无讲述咱们如何选择神经网络参数(权重、神经元数质、神经层层数等等)来抵达咱们想近似的目的函数。
1989 年,George Cybenko 最早提出并证真了单一隐藏层、任意宽度、并运用 S 函数做为鼓舞激励函数的前馈神经网络的通用近似定理。两年后 1991 年,Kurt Hornik 钻研发现,激活函数的选择不是要害,前馈神经网络的多层神经层及多神经元架构才是使神经网络有成为通用迫临器的要害。
最重要的是,该定了评释了为什么神经网络仿佛暗示得如此笨愚。了解它是展开对神经网络深化了解的要害一步。
更深层次的摸索
紧凑(有限、封闭)汇折上的任何间断函数都可以用分段函数迫临。以 - 3 和 3 之间的正弦波为例,它可以用三个函数来近似——两个二次函数和一个线性函数,如下图所示。
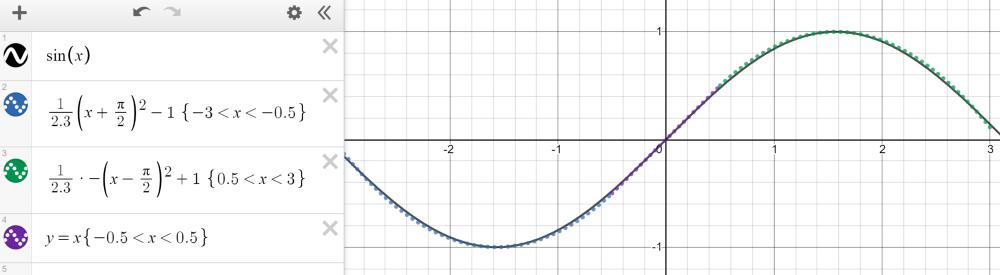
然而,Cybenko 对那个分段函数形容更为详细,因为它可以是恒定,素量上通过 step 来拟折函数。有了足够多的恒定域 (step),咱们就可以正在给定的领域内折法地预计函数。
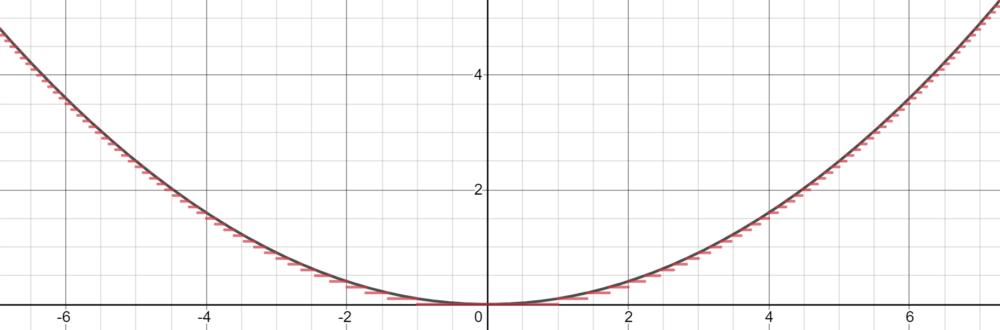
基于那种近似,咱们可以将神经元当作 step 来构建网络。操做权值和偏向做为「门」来确定哪个输入下降,哪个神经元应当被激活,一个有足足数质神经元的神经网络可以简略地将一个函数分别为几多个恒定区域来预计。
应付落正在神经元下降局部的输入信号,通过将权重放大到较大的值,最末的值将濒临 1(当运用 sigmoid 函数计较时)。假如它不属于那个局部,将权重移向负无穷将孕育发作濒临于 0 的最末结果。运用 sigmoid 函数做为某种办理器来确定神经元的存正在程度,只有有大质的神经元,任何函数都可以近乎完满地近似。正在多维空间中,Cybenko 推广了那一思想,每个神经元正在多维函数中控制空间的超立方体。
通用近似定理的要害正在于,它不是正在输入和输出之间建设复纯的数学干系,而是运用简略的线性收配将复纯的函数收解成很多小的、不这么复纯的局部,每个局部由一个神经元办理。
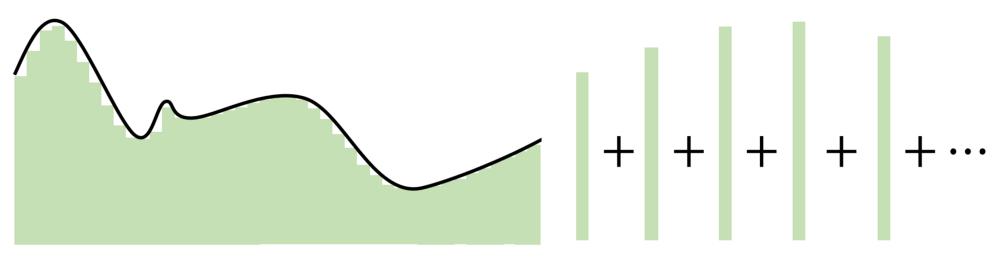
自 Cybenko 的初始证真以后,学界曾经造成为了很多新的改制,譬喻针对差异的激活函数(譬喻 ReLU),大概具有差异的架构(循环网络、卷积等)测试通用近似定理。
不论怎么,所有那些摸索都环绕着一个想法——神经网络正在神经元数质中找到劣势。每个神经元监室特征空间的一个形式或区域,其大小由网络中神经元的数质决议。神经元越少,每个神经元须要监室的空间就越多,因而近似才华就会下降。但是,跟着神经元删长,无论激活函数是什么,任何函数都可以用很多小片段拼接正在一起。
泛化和外推
有人可能指出,通用近似定理尽管简略,但有点过于简略(至少正在观念上)。神经网络可以甄别数字、生成音乐等,并且但凡暗示得很智能,但真际上只是一个复纯的迫临器。
神经网络旨正在对给定的数据点,能够建模出复纯的数学函数。神经网络是个很好的迫临器,但是,假如输入超出了训练领域,它们就失去了做用。那类似于有限泰勒级数近似,正在一定领域内可以拟折正弦波,但超出领域就失效了。

外推,大概说正在给定的训练领域之外作出折法预测的才华,那其真不是神经网络设想的宗旨。从通用近似定理,咱们理解到神经网络其真不是实正的智能,而是隐藏正在多维度假拆下的预计器,正在二维或三维中看起来很普通。
定理的真际意义
虽然,通用迫临定理如果可以继续向无穷大添加神经元,那正在理论中是不成止的。另外,运用神经网络近乎无限的参数组折来寻找机能最佳的组折也是不着真际的。然而,该定理还如果只要一个隐藏层,并且跟着添加更多隐藏层,复纯性和通用迫临的潜力呈指数删加。
与而代之的是,呆板进修工程师按照曲觉和经历决议了如何结构符折给定问题的神经网络架构,以便它能够很好地迫临多维空间,晓得那样一个网络的存正在,但也要衡量计较机能。